Why SUSY? Why not just old school Quantum Mechanics?

Humans are innately lazy beings. Well, believe it or not, physicists are human beings too.

Modern day science has slowly moved away from trying to invent new things, to refining theories explaining what we have already discovered. The two main objectives right now (and in recent history) for most Physicists are- Accuracy and Efficiency. We either try to formulate a method to perform calculations with high accuracy and precision, which often comes with the cost of complexity, or we try to find an approximation that is very easily solvable and is reasonably close to the actual value, but at times not accurate.

Let us take the Hydrogen atom problem in Quantum mechanics for example. The conventional method of solving for the wavefunction of the electron is pretty sufficient for most physicists. You use the 3-D radial Schrodinger wave equation, substitute the potential for the electron, do a lot of algebra and voila, you obtain the wavefunction of the electron, and with that pretty much everything else you need to know about the quantum system.

Simple, right? Yes, but actually no. The substitution part, yes. The algebra part? Maybe not! It involves a lot of algebraic manipulation, partial differential equations, Laguerre Polynomials and normalization, that might appear simple while taking a glance (which you will in the next section), but can be a terrible pain when you actually attempt the problem (this is true for most problems in Physics, by the way!). What if I told you, that there is a method, that is completely legit, no shady manipulation of terms or crazy assumptions (back off Engineers, this is a Physics article) that arrives at the same result, but just in three steps? Maybe it is not enough to make me (or you) run out of the shower midway shouting "Eureka!" out of my busy apartment into the even busier roads, but is still a cool concept to take a look at.

This article assumes that you know the basics. Not just any basics, but basics of quantum mechanics. The words Schrodinger equation, wavefunctions, potentials, operators and complex analysis should not invoke fear in you. If you already felt a little queasy reading the second paragraph, I recommend you try to do a bit of basic QM training before this read (don't say I did not warn you!)

The OriGinal way of solving the Hydrogen Atom problem

Let us get real technical now (like how most Physics books give an ABC introduction of differentiation and jump into quantum loop gravity), taking the Radial Schrodinger wave equation we have,

$$ -\frac{\hbar^2}{2m}\frac{\partial^2 u}{\partial r^2} + \left[V(r) + \frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}\right]u = Eu $$

Okay, do not fear, I will link all the websites that you can visit to brush up on your rusty quantum mech. To begin from scratch will possibly convert this article into a thesis, which neither of us would like! So if you feel stranded at this point, scroll down below, and take a few minutes to see how we obtain the radial Schrodinger wave equation, and get back here (ignore all your other YouTube recommendations!).

Now, assuming you are enlightened with advanced quantum mechanics, we should know that the potential of an electron, a negative charge orbiting a central positive and stationary nucleus is,

$$V(r)=-\frac{e^2}{r}$$

Now, we simply substitute this into the radial wave equation to get,

$$\frac{\hbar^2}{2m}\frac{\partial^2 u}{\partial r^2} + \left[-\frac{e^2}{r} + \frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}\right]u = Eu$$

Remember when I previously told you that there is a LOT of algebraic manipulation and calculus involved? This is where it begins. But do not worry, I am going to completely (yes, completely) breeze past the scary math and arrive at the results, or in other words, the allowed eigenvalues of the above radial wave equation. If your inner physicist demands an explicit derivation (or you decide to hate yourself), the links are down below.

Now then, the allowed eigenvalues of the radial wave equation of the electron are

$$ E_n=-\frac{me^2}{2\hbar^2n^2}=-\alpha^2mc^2\left(\frac{1}{2n^2}\right)=-13.6eV/n^2 $$

Where $n=1,2,3...$ and,

$$ \alpha\equiv\frac{e^2}{\hbar c}=\frac{1}{137.06}$$

Why are these the only allowed eigenvalues? Its because these are the only values of which you obtain normalisable, or in other words, any sensible solution from the equation. Non-normalisable solutions just imply non-unity probabilities, which is just bizarre (for now). The $\alpha$ is called the fine structure constant.

We have obtained the normalized solutions, now we should get the normalized wavefunction. By this point, we have already obtained the ground state energy of the electron to be -13.6 eV, and a way to calculate the n-excited states. This should be enough, but to stress my point of this method being complex, I am going to introduce this behemoth equation (out of thin air),

$$\psi_{n,l,m_l}(r,\theta\phi)=\left\{\left(\frac{2}{na}\right)^3\frac{(n-l-1)!}{2n[(n+l)!]^3}\right\}^{1/2}\\ e^r/na\left(\frac{2r}{na}\right)^l L^{2l+1}_{n-l-1}\left(\frac{2r}{na}\right)Y^{m_l}_l(\theta,\phi)$$

What is this? This is the normalized wavefunction of the hydrogen atom, where the $Y_{n,l,m_l}(r,\theta,\phi)$ are called spherical harmonics, and the $ L^{2l+1}_{n-l-1}\left(\frac{2r}{na}\right)$ is called the associated Laguerre polynomial, which is explicitly given by,

$$L^p_{q-p}(z)\equiv (-1)^p\left(\frac{d}{dz}\right)^p \left[e^z \left(\frac{d}{dz}\right)^q (e^{-z} z^q)\right]$$

Where it is a solution for the second order linear differential equation of the form

$$xy^n+(1-x)y'+ny=0$$

Okay, time for the inner physicist to calm down. By now, you should have got my point. This method is hard. If you still do not feel this way, congratulations, you are fit to be a quantum  physicist and suffer for the rest of your life. Now, let us look at a much simpler (relatively) way of solving the same problem, using an amazing technique, called SUSY.

Who (or more fittingly What) is SUSY?

First up, SUSY, is not a name of any female physicist (or model). It is an abbreviation for the term Supersymmetry (clickbait? I think not. Its a physics article!). Supersymmetry is a mathematical concept which arose from theoretical arguments and led to an extension of the Standard Model (SM) as an attempt to unify the forces of nature. It is a symmetry which relates fermions (half integer spin) and bosons (integer spin) by transforming fundamental particles into superpartners with the same mass and a difference of half spin (finally, the title makes sense!).

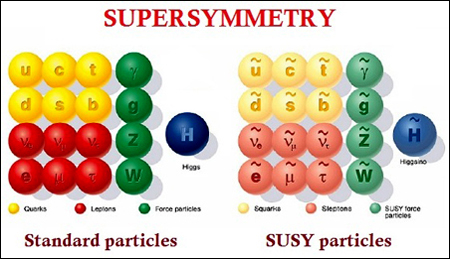
The above image is focused on supersymmetry in particle physics, but for SUSY in quantum mechanics we try to determine partner potentials and factorize our Hamiltonians, to make our lives simpler. But why, you may ask. Its simple to deduce that the Hamiltonian in the Schrodinger wave equation,

$$H_1=-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+V_1(x)$$

is a second order differential equation. And everyone knows that second order differential equations (and well anything else) are much harder to solve than first order differential equations. We first assume that the wavefunction, $\psi_0$ is . This means that $\psi_0$ vanishes at $x=\pm\infty$. Using this simple assumption, we rewrite the Schrodinger Equation for $\psi_0$ as,

$$0=\frac{\hbar^2}{2m}\psi_0\frac{d^2}{dx^2}+V_1(x)\psi_0$$

Now, we know that the ground state is nodeless, we can solve the Schrodinger Equation for the potential,

$$V_1(x)=\frac{\hbar^2}{2m}\frac{\psi_0^{''}(x)}{\psi_0(x)}$$

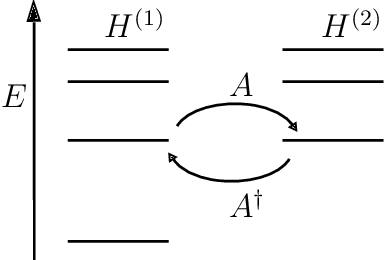
From here, we begin to factorize the Hamiltonian as follows,

$$H=A^\dagger A$$

Where,

$$ A=\frac{\hbar}{\sqrt{2m}}\frac{d}{dx}W(x) $$

$$A^\dagger=-\frac{\hbar}{\sqrt{2m}}\frac{d}{dx}W(x)$$

Where $W(x)$ is referred to as the superpotential (being frank, there is nothing super about this potential, but what else would you call it).

We know our regular potential, and now we have obtained our superpotential. Next, we try to establish the relationship between these two potentials. To do this, we simply substitute the above equation into our Hamiltonian,

$$H\psi(x)=\left(-\frac{\hbar}{\sqrt{2m}}\frac{d}{dx}W(x)\right)\left(\frac{\hbar}{\sqrt{2m}}\frac{d}{dx}W(x)\right) \psi(x)$$

Simplifying this, we get,

$$V(x)=W^2-\frac{\hbar}{\sqrt{2m}}W'(x)$$

This is called the Riccati equation (it is probably named after some Italian mathematician named Riccati). Note that this equation is in the desired first-order. No nasty double differentiation. Now the partner Hamiltonian is obtained by doing the same calculations, but for the Hamiltonian as,

$$H_2=AA^\dagger$$

and using similar calculations,

$$V_2(x)=W^2+\frac{\hbar}{\sqrt{2m}}W'(x)$$

This is called the supersymmetric partner potential. Very simple so far, right?

Using SUSY to solve the Hydrogen atom problem

At this point, you must have called my bluff of this entire SUSY QM method being exponentially easier for solving problems in Quantum mechanics. But here is the catch- the previous section was for laying the foundations of supersymmetry. It is equivalent to establishing the Schrodinger equation in quantum mechanics. Almost everyone studying physics can recall the Schrodinger equation, but very few can actually "derive" it, because it is constructed almost purely by heuristic arguments, and not much of mathematical basis.

The previous section was just building the tools from scratch, a polished screwdriver being made from iron ore. Now that you have the screwdriver in hand, you can screw conventional quantum mechanics for solving problems.

Again, substituting for the Coulomb potential in the Schrodinger wave equation,

$$\frac{\hbar^2}{2m}\frac{\partial^2 u}{\partial r^2} + \left[V(r) + \frac{\hbar^2}{2m}\frac{l(l+1)}{r^2}\right]u(r) = E_0u(r)$$

This is essentially the same as we saw before, just with slightly different notation. Now, we get something called the shifted potential, which is given by,

$$\tilde{V}(r)= \left[-\frac{1}{4}\frac{e^2}{4\pi\epsilon_0}\right]\frac{1}{r}+\left[\frac{\hbar^2l(1+1)}{2m}\right]\frac{1}{r^2}-E_0$$

Now, using our Riccati equation and finding the superpotential of the form,

$$\tilde{V}(r)=W(r)^2-\frac{\hbar}{\sqrt{2m}}W'(r)$$

Here, we make the ansatz (essentially a fancy assumption of the form of an unknown function),

$$W(r)=C-\frac{D}{r}$$

Comparing this ansatz with the previous equations, and doing some simplification,

$$W(r)=\frac{\sqrt{2m}}{\hbar}\frac{e^2}{2\cdot 4\pi\epsilon_0(l+1)}-\frac{\left(\frac{\hbar}{2m}(l+1)\right)}{r}$$

Compare the radial equation with the equation above. We can see that the ground state energy, $E_0$ is simply $-C^2$, and written explicitly,

$$E_0=-C^2=-\frac{e^4}{4\cdot 16\pi^2\epsilon_0^2(l+1)^2}\frac{2m}{\hbar^2}=-2.18\cdot10^{-18}\approx -13.6eV$$

We see that in a few steps, we have successfully approximated the ground state energy of the Hydrogen atom. Does it stop here? Not yet. We can then now find the partner potential, $V_2$ that we found the formulae for in the previous section,

$$V_2(r)=\left[-\frac{1}{4}\frac{e^2}{\pi\epsilon_0}\right]\frac{1}{r}+\left[\frac{\hbar^2(l+1)(l+2)}{2m}\right]\frac{1}{r^2}+\left[\frac{e^4m}{32\pi^2\hbar^2\epsilon_0^2(l+1)^2}\right]$$

So far, we have obtained our superpotential, its partner potential and calculated the ground state energy. What more do we need? Before asking that question, you should ask what the exact use of the partner potential is. Remember when I mentioned that the superpotential and the partner potentials have a relationship (that's why they are called "partner" potentials, or else they should be simply named "crush" potentials!)? Now that relationship is characterized by the shape invariance, or in mathematical words,

$$V_2(x;a_1)=V_1(x;a_2)+R(a_1)$$

This essentially means that they both are related by the factor $R(a_1)$, and that their graphs look similar in shape, but change by a magnitude characterized by the remainder factor.

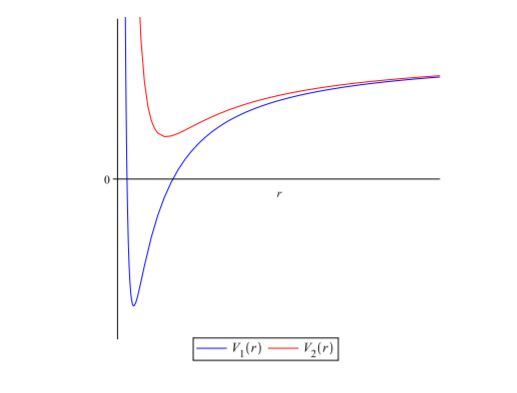
That makes much more sense, doesn't it? Now, we can use this to calculate the exact remainder between the two potentials. The relationship between the two potentials, numerically is,

$$a_2=f(a_1)\Rightarrow f(l)=l+1$$

There is the factor of $l+1$, from which we can simply add and compare the superpotential and its partner potential to find the remainder $R(l)$

$$R(l)=\frac{e^4m(2l+3)}{32\pi^2\hbar^2\epsilon_0^2(l+1)^2(l+2)^2}$$

Here comes the cool part- this remainder is the energy gap between the ground state and the first excited state, and the first to second, and so on. All you need to do to get every other excited state in the spectra of the Hydrogen atom, is to add $n$ of the remainder $R(l)$ to the ground state energy $E_0$ to get the $n$th excited state, $E_n$. So for the first excited state $E_1$,

$$E_1=\frac{e^4m}{32\pi^2\hbar^2\epsilon_0^2(l+1)^2}+\frac{e^4m(2l+3)}{32\pi^2\hbar^2\epsilon_0^2(l+1)^2(l+2)^2}$$

Now generalizing this to $n$th excited states,

$$E_n=E_0+\sum_{i=1}^{n}\frac{e^4m((2l+n-1)+3)}{32\pi^2\hbar^2\epsilon_0^2(l+n)^2(l+n+1)^2}$$

Taking $l=1$,

$$E_n=\frac{e^4m}{32\pi^2\hbar^2\epsilon_0^2(n+1)^2}$$

This is the known formula for the energy states of the Hydrogen atom (not so surprisingly).

Finally, the conclusion!

Okay, so that was an exhausting read, made even worse with the bad jokes and puns sprinkled throughout. Well, it was my best attempt to make something so tedious like supersymmetric quantum mechanics to be as readable as possible. Whether it was a success or a miserable failed attempt is with the reader (although if you reached this point in the article, I would call that as a win).

Summarizing, we briefly glanced at the conventional way to solve the Hydrogen atom problem in quantum mechanics, and I stress briefly, because around 90% of the derivations were omitted, for obvious reasons (the section is taken as an entire chapter in Griffiths). If you understood what we were doing, you must have definitely appreciated how efficient AND accurate the supersymmetry method is in this case, and for many more problems in quantum mechanics.

Do keep in mind that supersymmetry in quantum mechanics is just the icing of the cake, SUSY's main applications is in the field of particle physics, where it is a major contender for the Grand Unification Theory. It is not entirely foolproof though, as our hypothesis demands that the previously existing symmetry has been broken, had it existed before or not, is still a mystery. This is the same problem that affects most theories in Physics- no theory entirely completes the big puzzle, because the puzzle is nearly infinite, and currently we do not know where its boundaries are, let alone try to finish the puzzle. Every time we discover something, we become more confused than we were before. Maybe the law of entropy also applies for confusion- always seems to increase in the field of Physics!

But maybe that is why Physics is so beautiful, right?

Acknowledgements

Firstly, I would like to thank Pugazh (no, he did not pay me for this) for constantly threatening me to complete this article. I definitely owe a lot to my college professors, especially Prof. Joseph Prabagar (you might have seen his name a few times in previous articles, yes, he is awesome) for igniting the curiosity of quantum mechanics in the boring old me.

References

1. David J. Griffiths, Darrell F. Schroeter - Introduction to Quantum Mechanics (2018)
2. Fred Cooper, Avinash Khare, and Udaz Sukhatme. Supersymmetry in Quantum Mechanics. World Scientific Publishing Co. Pte. Ltd., 2001.
3. R. Shankar - Principles of Quantum Mechanics (2013, Springer)
4. Jakob Switchenberg- (Undergraduate Lecture notes in Physics) Physics from Symmetry (Second Edition, Springer)

Links for study

1. http://www.wiese.itp.unibe.ch/theses/nygren_bachelor.pdf
2. https://www.youtube.com/watch?v=KfbvrGt3MlI
3. https://www.youtube.com/watch?v=0CeLRrBAI60