When Born-Oppenheimer Fails
Prelude : Quantum Chemistry is hard
Quantum mechanics hinges itself on a beautiful equation that derives the possible states of a microscopic system : the Schrodinger equation.
$$\hat{H} \psi = E \psi$$
This "state" indicates the manner in which the probability density of a system is distributed. Specifically, the Schrodinger equation derives energy states, which are wavefunctions obtained when we're interested in measuring energy. The energy "operator", which acts on the wavefunction to derive energy states is formulated based on the conditions in which we release our system. Operator equations such as these are typically partial differential equations, which are differential equations having many variables. To solve these equations, we try to separate the variables and create individual single-variable equations. For each new particle added to the system, 3 new variables are added to the mix, one for each position co-ordinate. Furthermore, the form of the energy operator becomes significantly more complex, adding a new kinetic energy term and several potential energy terms to the mix.
$$ \hat{H} =\frac{-1}{2} \sum_{n} \nabla ^{2}_{n} + \frac{-1}{2} \sum_{\alpha} \nabla ^{2}_{\alpha} + \sum_{n} \sum_{m \neq n} \frac{1}{r_{mn}} + \sum_{n} \sum_{\alpha} \frac{Z_{\alpha}}{r_{\alpha n}} + \sum_{\alpha} \sum_{\beta \neq \alpha} \frac{Z_{\alpha} Z_{\beta}}{r_{\alpha \beta}}$$
Quantum chemistry applies the great machinery of quantum mechanics to atoms and molecules, which are complex many-particle systems. Each atom that comprises a molecule has a nucleus and several electrons. Each particle and each interaction between particles contributes a term to the energy operator. Any attempts made to solve such a complicated Schrodinger equation would be futile and meaningless since small perturbations to the initial conditions send us back to square one. To simplify this problem enormously, Max Born and J Robert Oppenheimer treated the system as though the motions of electrons are independent of the motion of nuclei (removing the second summation of the above ugly expression), the justification being that nuclei are so heavy and so slow compared to electrons that their motions would barely alter the wavefunctions of electrons. In effect, the wavefunctions of electrons and nuclei are treated as separable, making it easier to solve the equation.
$$ \hat{H}_{electronic} \psi_{electronic} = E_{electronic} \psi_{electronic}$$
The Born-Oppenheimer approximation (also called the Adiabatic Model) is arguably the best mathematical approximation that scientists have come up with for molecules. Most quantitative theories in chemistry and solid state physics that deal with bonding and formation of molecules use the Born-Oppenheimer approximation and match experimental results with striking accuracy. But, of course that's boring. Let's instead talk about rebels that disobey this rule and try to think about why.
Case 1 : Carbon Nano-Tubes
Certain kinds of lattices and solids fail to conform to the Born-Oppenheimer Approximation. This is because they have a short vibrational period of oscillation (i.e. a high frequency of vibration). They vibrate fast enough for the nuclear motion to start becoming significant enough for the Born-Oppenheimer approximation to start falling apart. This phenomena was first noticed by Walter Kohn in 1959 and is hence referred to as a Kohn Anomaly.
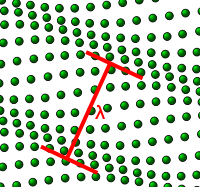
Carbon Nanotubes are one such example. They are small (their radii measure in nanometers) cylindrical tubes comprised of carbon atoms. They have a short period of oscillation and a long relaxation time (i.e. time taken between successive collisions of electrons), which makes them ideal candidates to showcase Kohn Anomalies. Carbon Nanotubes have a wide range of applications. Physicists want to use them to verify their hypotheses on fundamental phenomena such as spin-orbit coupling and engineers enjoy messing around with any material that has semiconductor properties. Hence it becomes important to develop models that don't conform to the Born-Oppenheimer Approximation.

Case 2 : Our Eyes
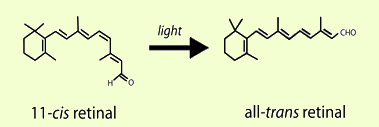
Once the chemical process of vision was identified to be the conversion of rhodopsin's cis retinal to an all trans form, chemists, biologists, physicists and engineers became interested in the peculiar dynamics of the underlying process. The photochemical process of rhodopsin excitation is an ultrafast conversion of the photons' energy into chemical energy. These processes are non-adiabatic, they don't agree with the assumptions made in the Born-Oppenheimer approximation.
Leaving us...where?
Interesting case studies like these let us know that no matter what approximations we make, nature always has a unique system in store for us that can defy expectations and showcase unusual results. Scientists have come up with interesting models and schemes to tackle the non Born-Oppenheimer problem (a discussion of which would be far too theoretical for the purposes of this article), however it is interesting to note that they too use a good amount of approximation and simplification leaving room for the discovery of more interesting anomalies and further refinement of the underlying theorem.
As the statistician George Box once said, "All models are wrong, but some are useful". It is a sobering thought that each theory and approximation we come up with can be quickly defied by nature, yet it is astonishing that they work for most cases.
References
Breakdown of BO approximation in SWCNTs : https://arxiv.org/pdf/0901.2947.pdf
Non-adiabatic dynamics of vision : https://pubmed.ncbi.nlm.nih.gov/20864998/
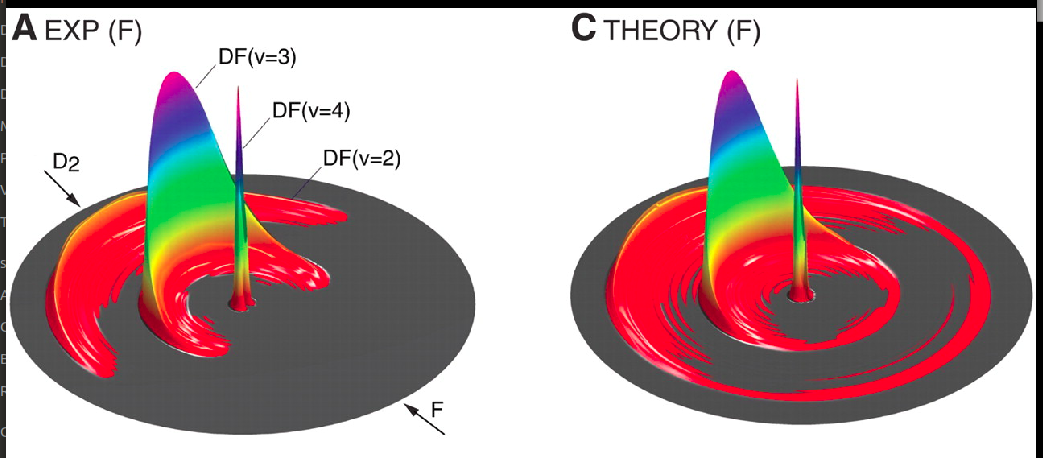
Cover image taken from an article on breakdown of Born-Oppenheimer approximation in fluorine + deuterium reaction : https://science.sciencemag.org/content/317/5841/1061
