How much do you really know?

Raise your hand if you know this guy:

If you don't, shame on you. His name is Claude E. Shanon. He's a genius.
The first time I was introduced to his work, it lit my mind on fire.

Because Claude Shanon did something incredible–he defined what information is.
And I'm not talking about some vague philosophical definition involving the mind, thought, perception, and the meaning of life. He literally wrote it down:
$$I(X) = -\log{\mathbb{P}(X)}$$
Information
Unless you're already familiar with information theory, that probably doesn't make sense yet. So let's do a quick breakdown:
- $I(X)$ measures the information (more specifically, it's called the self-information) of an event $X$.
- $log$ is well, just a regular logarithm function. There's an interesting piece of information (see what I did there) surrounding the choice of the base for the $log$, which I'll talk about a little later. But for simplicity, assume that it's base $e$, which would make $log$ represent the natural logarithm
- $\mathbb{P}(X)$ is the probability of the event $X$ occurring.
So why is this a good definition for information?
Well, think about some of the properties of a good definition of information.
Ideally, events that are pretty normal and naturally occurring (high probability) should carry less "information" than rare events.
For example, the sun rises every day. What do learn from that? Not much.
But suppose you look up and see this:

That's a solar eclipse. It doesn't happen everyday (at least, not on earth). Just by noticing the eclipse, you'd know the relative positions of the sun, moon, and earth.
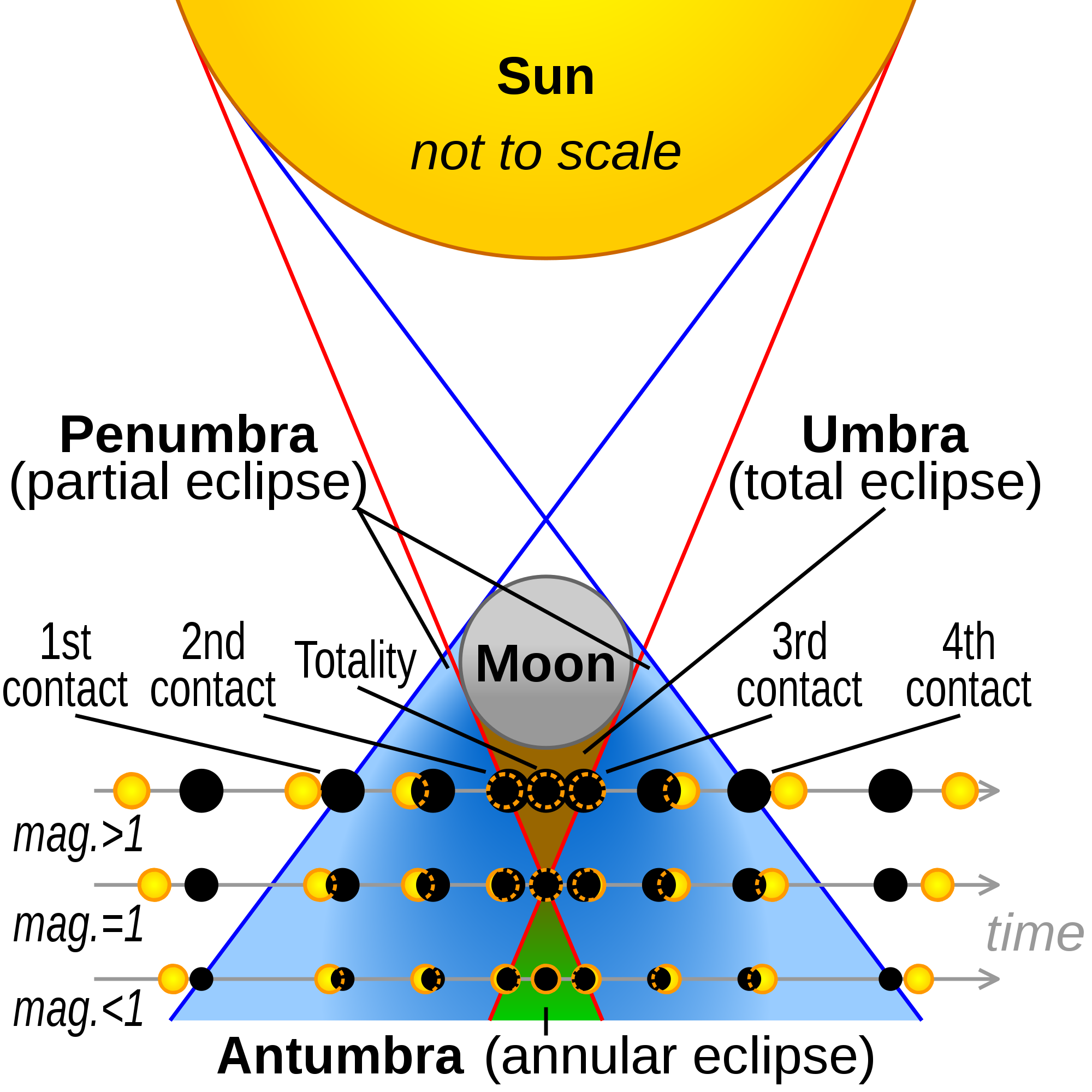
In other words, a solar eclipse happening gives you more "information" than the sun rising.
Does this property of high-probability events having low information check out with Claude Shanon's definition? Take a look at the plot for $y = -\log{x}$:
So yes, $I(X) = -\log{\mathbb{P}(X)}$ looks good.
What Does The $\log$ Say?
If you're wondering what the base of the logarithm signifies, wonder no more.
When we're measuring information, we need some common unit to measure how much information there is. Say, for example we want to use bits.
Here's the cool part: since bits are the number of base-2 digits required, using base-2 for the logarithm gives you $I(X)$ in bits.
Yes, the very same bits that your computer uses to measure how much it has to work to load those YouTube videos that you couldn't stop watching last night.

To illustrate how amazing this idea is, I'm going to calculate the information produced by Shaq score a three pointer.
Shaq has scored exactly 1 three (Source) out of the 22 attempts in his career.
$$ I(\text{Shaq scoring a three}) = -\log_2{\frac{1}{22}} $$
$$ \approx 4.45943161878 $$
About 4 or 5 bits. Which, to be honest, is far lower than I thought it would be.
Entropy
There's a small weakness with our definition of information– it only accounts for single events.
But single sample (or events) don't always tell you the full story.
Take a look at these 2 distributions:
Let's call the random variable represented by the blue distribution $B$ and the random variable represented by the red distribution $R$.
Now let's say we sample from both distributions, and get a value of $-2$ for both $R$ and $B$.
Since we know the distribution of the random variables $B$ and $R$, we can calculate the information "released" by observing that they are both $-2$.
But there's a catch. According to the distribution, it's pretty likely that you'll get $-2$ if you sample $B$. In fact, it's the mean. When you look at the distribution of $R$, however, it's much lower.
So when we try to calculate information, we'll get that
$$ \mathbb{P}(R=-2) < \mathbb{P}(B=-2) $$
$$ \implies I(R=-2) > I(B=-2) $$
Ok, this kind of makes sense. It agrees with what we've established so far. But our conclusion about $R$ giving more information cannot extend to the entire distribution, only that one particular case where $B=-2$ and $R=-2$.
That sounds pretty useless then, right? Because claiming that sampling from $R$ would give you more information is completely ridiculous. $B$ and $R$ differ only by a constant. So they should theoretically have some quantity in common.
If you didn't follow, here's what I mean: Say you have 2 dice (because even though physicists have proved the convergence of Cauchy sequences in infinite dimensional Hilbert spaces and calculated the curvature of differentiable Riemann manifolds, the motion of a 6-faced regular solid is beyond the comprehension of physics and is therefore, 100%, unequivocally, random).
Both of them are fair, but the've been numbered differently. One of the die is numbered from 1-6, while the other is numbered from 3-8.

This sort of models the situation above. Both distributions are only separated by only by a constant, so they sampling from both distributions (rolling the dice) would, on average, produce the same amount of information.
If you didn't get the gist already, Claude Shanon was a genius, so he figured this out too. He defined a quantity which is common for both distributions– Entropy.

Again, this isn't some vague and abstract definition like those pop-science videos on YouTube that just can't seem to stop saying "Entropy is chaos".
No. Claude E. Shanon wrote the darn thing down:
$$ H = -\sum_i{\mathbb{P}(X=x_i) \log{\mathbb{P}(X=x_i)}} $$
Where $H$ represents entropy, and the random variable $X$ takes on the values $x_i$.
In the continuous case,
$$ H = -\int_{\mathbb{R}}{p(x) \log{p(x)}} $$
Where $p(x)$ is the probability mass function of a distribution.
Let's break that down. From now, I'll focus on the discrete case.
We know that the information produced by individual events sampled from two distributions messes the math up, so what else might work?
We could try to find the information released by the obtaining the mean (or median or mode) from a single random sample.
But again, the keyword there is single sample. So we still wouldn't get clues about the distribution as a whole.
What we'll use is the expected information. Which is exactly what it says it is– the expected value of information.
$$ \mathbb{E}[I(X)] $$
And we know how to calculate expected values!
$$ \mathbb{E}[I(X)] = \frac{\sum_i{I(X_i)}}{N}$$
So what's the total amount of information?
Let's see, event $x_i$ occurs with probability $\mathbb{P}(X = x_i)$. If we take $N$ samples, $x_i$ happens $N_i$ times. So,
$$ \mathbb{E}[I(X)] = \frac{\sum_i{I(x_i)}}{N}$$
$$ = \frac{\sum_i{N_i I(x_i)}}{N} $$
$$ = \frac{\sum_i{\mathbb{P}(X=x_i) N I(x_i)}}{N} $$
$$ = \sum_i{\mathbb{P}(X=x_i) I(x_i)} $$
$$ = -\sum_i{\mathbb{P}(X=x_i) \log{\mathbb{P}(X=x_i)}}$$
So I guess Claude Shannon, in a really meta way, didn't show that he knows a lot. He mathematically proved it.
