An Approachable Derivation of the Rayleigh-Jeans Law
Premise
We can consider a black body to consist of electromagnetic radiation in thermal equilibrium with the cavity walls. When they are in thermal equilibrium, the average rate of radiation emission equals their average rate of absorption of radiation.
The Rayleigh-Jeans theory was constructed on the notion that when the walls of an object are in thermal equilibrium, in other words, the temperature of the walls is equal to the "temperature" of radiation. We will see what we mean by the "temperature" of an electromagnetic wave.
If we take the walls of a cavity to consist of oscillating charged particles (about its equilibrium) coupled to a standing-wave mode of an electromagnetic field. This can be seen from Maxwell's theory of electromagnetic waves, which states that a moving charged particle radiates an electromagnetic wave. A point to be noted is that the oscillating charge's frequency is equal to the frequency of its coupled electromagnetic wave. So then, it is safe to say that in thermal equilibrium, the average energy of the oscillating charge is equal to the average energy of the coupled standing-wave mode of that electromagnetic field.
Now we can see that the oscillating particle has a quadratic potential energy, $H_{pot}$ of $\frac{1}{2}aq^2$ and a kinetic energy $H_{kin}$ of $\frac{p^2}{2m}$, so according to the equipartition theorem, in thermal equilibrium the average energy is,
$$ <H> = <H_{pot}> + <H_{kin}> = \frac12 k_B T + \frac12 k_B T=k_B T$$
Hence, the wave's energy is also taken to be $k_BT$ and can be thought to have a "temperature" of T. This forms the foundation of the Rayleigh-Jeans theory, following which we will derive the Rayleigh-Jeans formula.
Deriving the Rayleigh-Jeans Formula
We start off with the axiom that the energy distribution of black-body radiation does not depend on the cavity's shape (which can be proven experimentally). For ease of calculations, we take the shape of the cavity to be a cube. We also assume that the waves vanish at the walls, or in other words, do not pass through them.
The number of standing electromagnetic waves in a cube of length L needs to be calculated.
Let us take the wave equation for the standing electromagnetic wave,
$$ \frac{\partial^2E_x}{\partial x^2}+\frac{\partial^2E_x}{\partial y^2}+\frac{\partial^2E_x}{\partial z^2}+k^2E_x = 0 $$
Where $E_x=E_x(x,y,z)$ and $k=\frac{2\pi}{\lambda}=\frac{2\pi f}{c}$. Assuming that $E_x=u(x)v(y)w(z)$ (by variable separable method), we can separate Equation (2) into three ordinary differential equations of the type,
$$\frac{d^2u} {dx^2}+k^2_xu=0$$
Where $k^2=k^2_x+k^2_y+k^2_z$.
By inspection, we can see that Equation (3) is an equation for a simple harmonic oscillator and has the solution,
$$u(x)=B\cos k_xx+C\sin k_xx$$
Applying necessary boundary conditions so that $E_x$ or $u$ is 0 at $x=0$ and at $x=L$ leads to $B=0$ and $k_xL=n_x\pi$ where $n_x=1,2,3,...$, (since we are considering standing electromagnetic waves and look at only the positive region of the k-space) similar solutions are obtained for $v(y)$ and $w(z)$, giving the solution,
$$E_x(x,y,z)=A\sin (k_xx)sin(k_yy)\sin(k_zz)$$
Where, $$k^2=\frac{\pi ^2}{L^2}(n^2_x+n^2_y+n^2_z)$$ and $n_x$, $n_y$ and $n_z$ are positive integers.
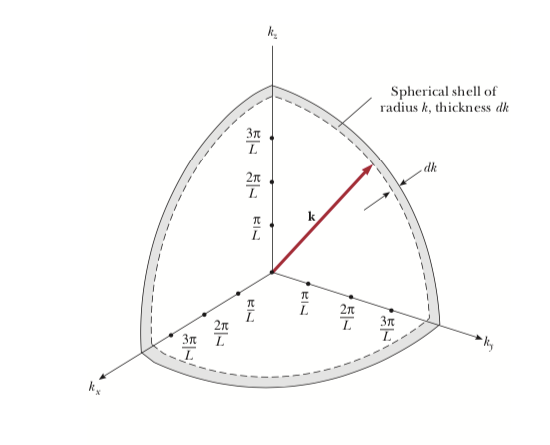
Now, we take equation (6) to give us the distance from the origin to a point in $k$-space or often called the "Reciprocal" space (due to the units of $k$ being $(length)^-1$).
Let us take a coordinate system corresponding to the $k$-space (shown in Figure 1), with the axes being $k_x$, $k_y$, and $k_z$. And we know that $k_x=n_x\pi/l$, $k_y=n_y\pi/L$, and $k_z=n_z\pi/L$, so the points in $k$ space are separated by $\pi/L$ along each axis, and there is one standing wave in $k$-space per $(\pi/L)^3$ of volume. The number of standing waves, $N(k)$ having wavenumbers between $k$ and $k+dk$ is then simply the volume between $k$ and $k+dk$ divided by $(\pi/L)^3$. The volume between $k$ and $k+dk$ is simply the volume of a spherical shell of thickness $dk$ multiplied by $1/8$ (since we need only the positive quadrant of the k-space, hence 1/4 of the volume of a sphere) so that
$$N(k)dk=\frac{\frac12 \pi k^2 dk} {(\pi/L)^3}= \frac{Vk^2dk} {2\pi^2}$$
Were $V=L^3$ is the volume of the cavity.
For any electromagnetic wave, there are two perpendicular polarizations for each mode, so Equation (6) should be increased by a factor of 2, becoming, $$\frac{N(k)dk}{V}=\frac{k^2dk}{\pi^2}$$ From using the expression $k=2\pi f/c$ to obtain $k$ and $dk$ and substituting in Equation (8) gives us $N(f)$, $$N(f)df=\frac{8\pi f^2}{c^3}df$$ And from this, the number of modes per unit volume between $\lambda$ and$\lambda + d\lambda$ can be derived from Equation (9) by using the expression $f=c/\lambda$ to get $\lambda$ and $d\lambda$ to get,$$N(\lambda)d\lambda=\frac{8\pi}{\lambda^4}d\lambda$$ Now, each mode of oscillation has energy of $k_BT$, so the energy in the range $\lambda$ to$\lambda+d\lambda$ is $k_BTN(\lambda)d\lambda$. Hence the energy density in this region is,
$$u(\lambda)d\lambda = k_BTN(\lambda)=\frac{8\pi k_BT}{\lambda^4}d\lambda$$
This is the Rayleigh Jeans expression for spectral density in the range$\lambda$ to $d\lambda$ Considering the energy to be a continuous variable, then the average energy per oscillator is $k_BT$ and the Rayleigh Jeans formula for $u(\lambda)$ holds true. The Rayleigh Jeans formula also behaves perfectly well for long wavelengths in the electromagnetic spectrum. It also agrees with the Wien's scaling formula,$$u(\lambda)=\frac{8\pi k_BT}{\lambda^4}=\frac{f(\lambda T)}{\lambda^5}$$However, we will see in the next section why this is not a correct scaling function.
Failure of the Rayleigh-Jeans theory in explaining the Stefan-Boltzmann Law
Incorrect Scaling function
From the previous equation for the scaling function, we can see that $f(\lambda T)=8k_BT$. So from this, we can notice that as $\lambda$ decreases, u($\lambda$) also increases. This means that the higher the temperature, the lower the wavelength waves are emitted. For example, a campfire emits many short-wavelength microwaves (which is very deadly, but thankfully that isn't how things work in nature) according to this law. Hence, the law fails in this regard.
The Ultraviolet Catastrophe
Inspecting the Rayleigh-Jeans formula and attempting to find the total energy density (by integrating with appropriate limits) of the black-body gives us an exciting result,
$$ u=\int_{\infty}^{0}=u(\lambda)d\lambda=\int_{\infty}^{0}\frac{8\pi k_B T}{\lambda^4}d\lambda=\infty $$
Here we see that the energy density is infinite, which is easy to figure out that this is nonsensical. It implies that if a cavity filled with radiation radiates an infinite amount of energy. This was named by Paul Ehrenfest as the "Ultraviolet Catastrophe" However, Stefan found out that the energy radiated is proportional to $T^4$. Hence, explaining the Stefan-Boltzmann Law using the Rayleigh-Jeans formula for energy density will end in vain.
Consequences
As the Raleigh-Jeans formula failed to address shorter wavelengths, Planck decided to use a different approach to explain the black body radiation curve. He chose not to assume that an oscillator's average energy in the wall to be $k_BT$. He knew how $u(\lambda)$ varies for short wavelengths, using Wien's formula, and wanted u($\lambda$) to be proportional to T for longer wavelengths. This lead to the formulation of Planck's formula, which perfectly described the radiation curve.
References
- Bowley, R., Sanchez, M. (1999). Introductory statistical mechanics. Oxford: Clarendon.
- Zemansky. (, 1957). Heat and Thermodynamics.
Reading List
- Modes of Oscillations, UMDPhysics
- Deriving the Rayleigh-Jeans Law,chem.libretexts.org
- The Rayleigh-Jeans Law and its Derivation,applet-magic.com
- Rayleigh-Jeans Law,wikipedia.org
- Equipartition Theorem,wikipedia.org
