Demolishing the Ether

Newton and Huygens were two guys with cool hairdos. They disagreed on light.

Newton (the guy with the cooler name) pushed forward the particle theory of light, while Huygens pushed forward the wave theory of light. Newton was winning because he was Newton. Huygens who?

Uh-oh. The year 1801. The not so young scientist Thomas Young experimentally showed light was a wave. Newton ducked this punch and the ref gave him two points. 1819. Some random military dude, Augustin Fresnel, instead of leading his army, led the wave theory of light and landed a Sunday punch on Newton. The wave theory of light was now recognized.

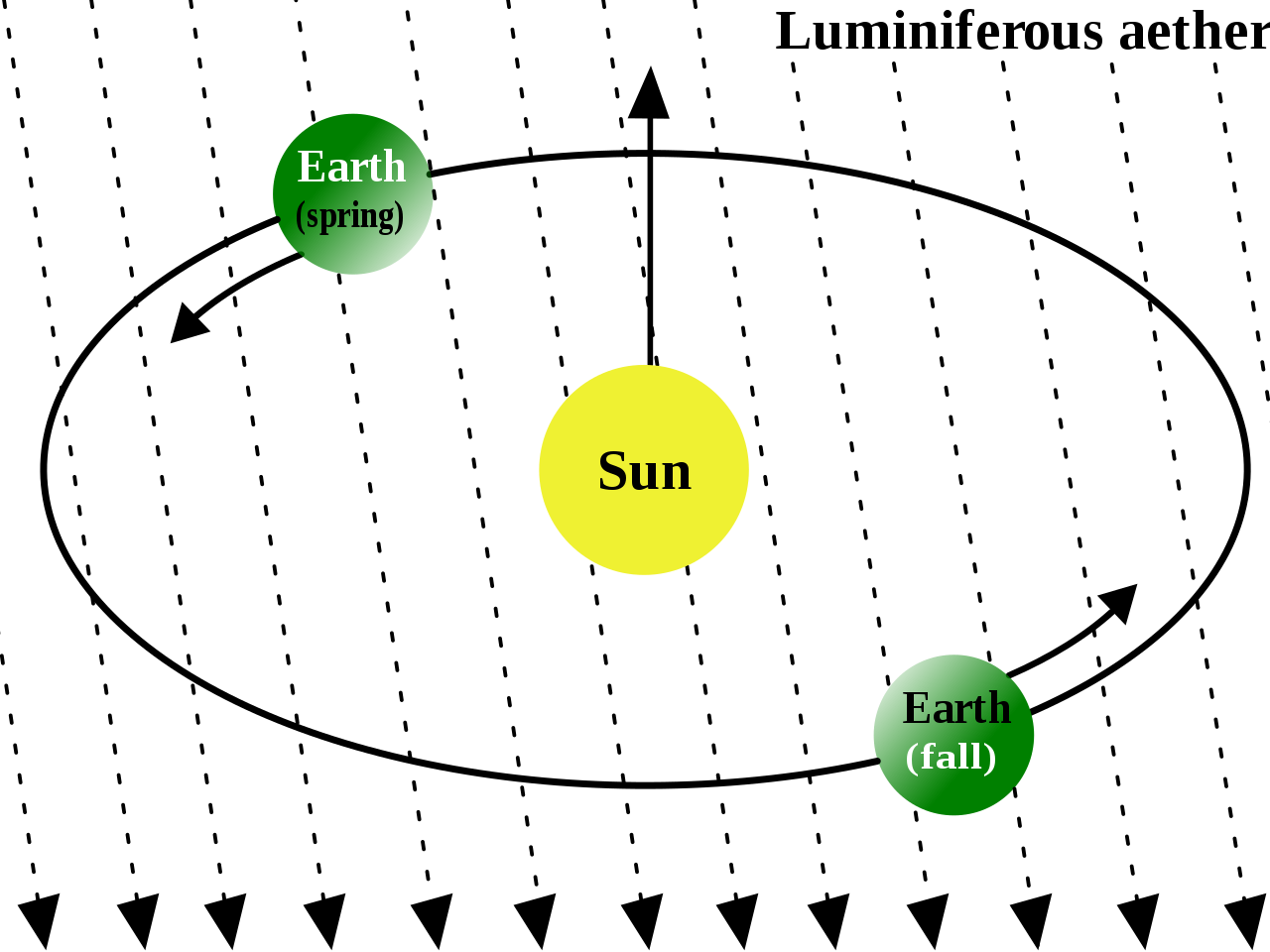
Scientists believed waves require a medium to travel. Previously, light could travel from the Sun to the Earth because it was a particle and particles can go wherever they want. But now, light is a wave. A wave needs a medium to travel. Look at sound. It doesn't travel in a vacuum. So, they proposed this new medium which permeates space. In other words, space isn't a vacuum. They called this the ether (or aether, not to be confused with the organic compound). And the speed of light in this aether is c (the normal thing, $3 \times 10^8$).

Knock, knock.

What's there?

Aether.

Aether, what?

Does aether exist or not?

M&M decided to do an experiment to address this question and to study the properties of aether. In 1887, they used a version of Michelson's interferometer to test the effects on the travel of light by aether. So the normal interferometer is quite complicated for a newbie. This one was messed up.

So I decided to provide this schematic diagram.

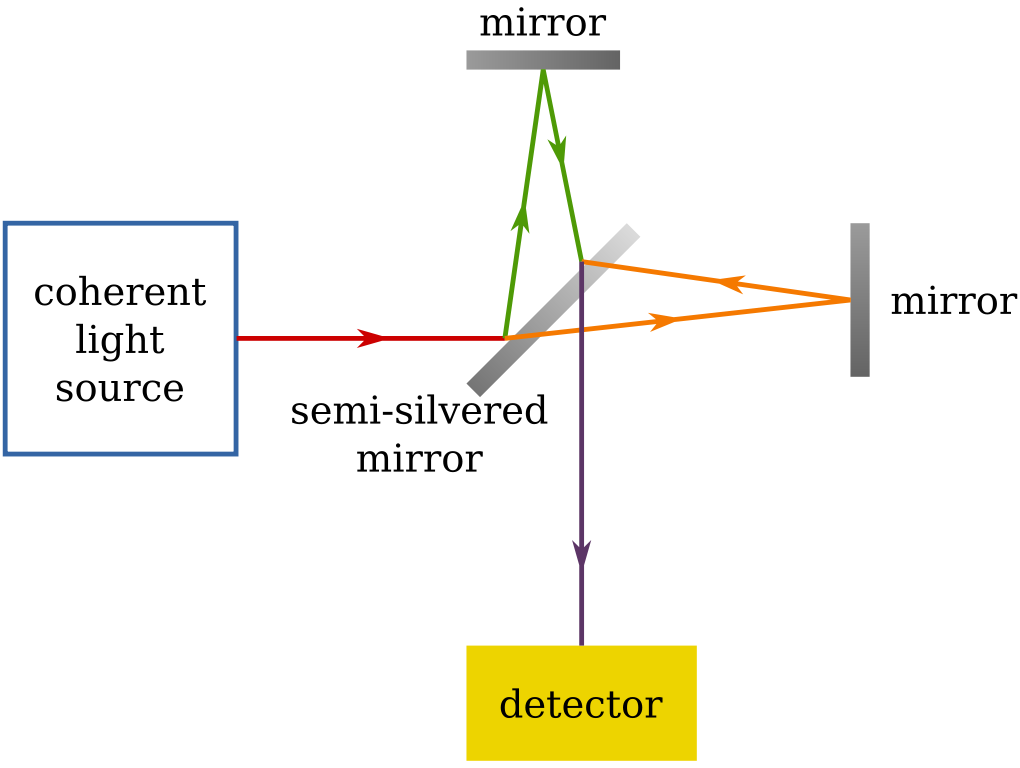
The light undergoes multiple reflections through the mirrors, so I haven't drawn the path of light.

For those who don't know what an interferometer is, A. A. Michelson (the first M) built this device to measure small changes in length with great accuracy by using fringe shifts. The light moves from the source. If it encounters a beam splitter, half of it is transmitted and half of it is reflected. Let's say if it encounters a mirror, it is completely reflected. The path length difference for the waves when they recombine at the telescope will give the phase difference. This can be used to calculate the shift. Using this device, Michelson showed that the meter was $1553163.5$ wavelengths of a red light produced by cadmium. This eventually led to the redefinition of the meter from a bar with two scratches to the modern definition based on light.

Back here, he teamed up with Edward Morely (the second M) to study aether. The Sun was assumed to be approximately stationary in aether. Hence, the speed of the interferometer should be v, the speed of the Earth around the Sun. The heavy slab on which the mirrors and splitters and apparatus was placed on was suspended on a pool of mercury to allow rotation about a vertical axis. This would change the orientation of the interferometer arms relative to the motion through aether. A fringe shift would indicate the presence of aether. To improve the possibility of a shift, the light was reflected multiple times (hence the multiple mirrors in each corner). This added complexity can be resolved to a simple interferometer with the effective length of each arm equal to $10\hspace{0.15 cm} m$.

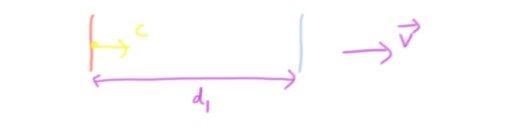
Let us assume that interferometer is being viewed in the aether reference frame. So it moves rightward with a speed $v$. Light goes to the mirror from the splitter and comes back. So the time taken for this, and hence the path length of light's travel along this arm is

$$ t_1 = \frac{d_1}{c+v} + \frac{d_1}{c-v} = \frac{2 c d_1}{c^{2} - v^{2}}$$

$$ L_1 = c t_1 = \frac{2 c^2 d_1}{c^{2} - v^{2}}$$

Looking at the diagonally opposite arm in the setup and the same procedure gives

$$ x = \frac{v t_2}{2} $$

$$ l = \sqrt{\frac{{t_2}^{2} v^{2}}{4} + {d_2}^2} $$

$$ t_2 = \frac{l}{c} = \frac{2 d_2}{\sqrt{c^{2} - v^{2}}} $$

$$ L_2 = c t_2 = \frac{2 c d_2}{\sqrt{c^{2} - v^{2}}} $$

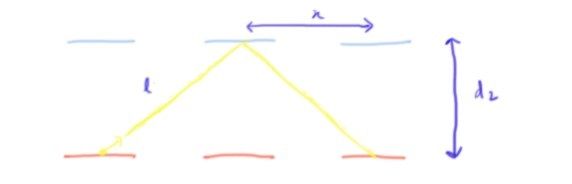
$d_1 = d_2$. So replacing them by $d$ won't change anything. The path difference is found to be

$$ \Delta L = L_1 - L_2 = \frac{2 c^2 d_2}{c^{2} - v^{2}} \left( 1 - \sqrt{1-\frac{v^{2}}{c^{2}}}\right)$$

Applying the binomial expansion, we get

$$ \Delta L = \frac{d v^2}{c^2} $$

Hence, the phase difference, which determines the fringe pattern produced by light is

$$ x = \frac{\Delta L}{\lambda} = \frac{d v^2}{\lambda c^2} $$

$$ shift = \frac{2 d v^2}{\lambda c^2} $$

Evaluating this shift with the known values fetches,

$$ shift = \frac{2 \times 10 \times (29.8 \times 10^3)^2}{500 \times 10^{-9} \times (3 \times 10^8)^2} = 0.3946 m = 39.46 cm$$

This fringe shift is a little over a foot. It would have been obvious. But M&M could not observe a fringe shift! This meant that light does not interact with aether. No party. No Nobel for M&M. (However Michelson did get a Nobel in 1907, but that was for the invention of the interferometer.) Then a guy with a crazier hairdo pounced on this result to give a "Special Theory".