The Push of the Unperceived

Recently, the comet C/2018 Y1 (Iwamato) whizzed past the Earth. It was my first comet sighting in more than 8 years. It was very faint and could be viewed only with a visual aid. On looking at it through my binoculars, I spotted something strange.

This comet had two tails. I knew comets have an ion tail, which is predominantly visible, but this one had a faint, but clearly visible second tail. I know the comet's tail tends to point away from the Sun. This is because ionization of atoms in the comet feel the power of the Sun's repulsive effect. And it hence points away. But the comet I saw on that night had two tails pointing at literally an obtuse angle.

I found out that a comet, actually, has two tails. One is the ion tail, which points away from the sun. The other is the dust tail. The dust tail isn't visible to the naked eye, because it doesn't emit light like the ionized particles. How is this dust tail formed?

You may know that light is made of massless particles called photons. These photons can exert pressure. You may wonder how a massless object can exert pressure. But light has momentum. And hence it can exert pressure. The Sun's radiant energy can push the dust particles along the comet's path to give it its tail.

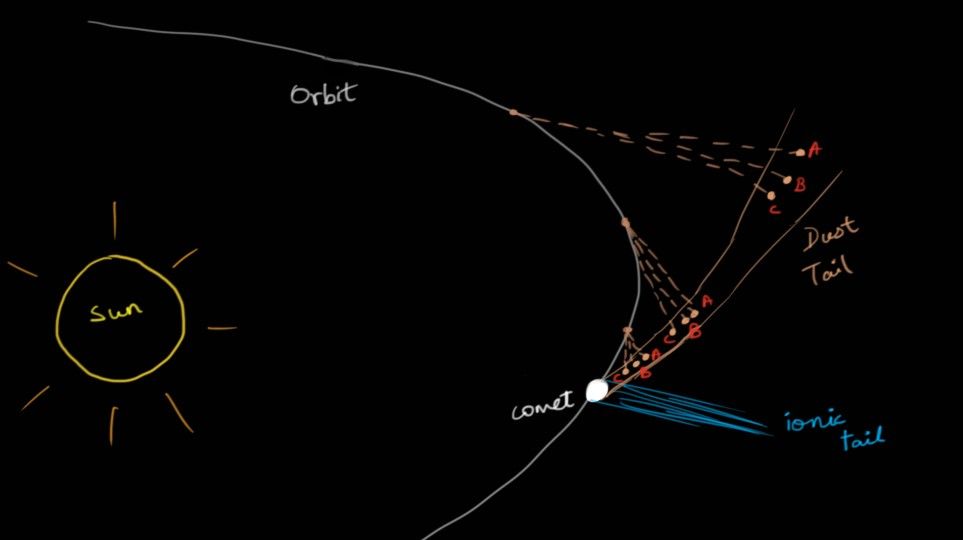
This picture gives an idea about the two tails. The path B is the straightest path, while A is curved away and C is curved towards. The dust particle in path B obviously had balanced forces acting on it which would explain its straight path. There are two major forces an ejected dust particle can face. One is the gravitational force from the Sun (the force from the comet/other bodies is negligible) and the other is the radiation pressure exerted by the sunlight.

Let us assume that the dust particle is roughly spherical. Let's assume the density of the matter making up the dust particle is $\rho = 3.5 \times 10^3 kg/m^3$. One last assumption is to assume that the dust particle absorbs all the energy that it intercepts from the Sun.

The radiation pressure is given by,

$$F_r = \frac{I A}{c}$$

where $I$ is the intensity of light and $A$ is the effective cross section area.

Let us take the power of radiation from the sun to be $P_s$.

$$F_r = \frac{\left(\frac{P_s}{4 \pi r^2}\right) \pi R^2}{c}$$

$r$ is the distance of the dust particle from the sun.

Moving on to the gravity equation, we have,

$$F_g = \frac{GMm}{r^2} = \frac{GM\left(\frac{4}{3} \pi r^3\right) \rho}{r^2}$$

Equating the two, we get

$$R = \frac{3 P_s}{16 \pi c G M \rho}$$

$$R = \frac{3 \times 3.9 \times 10^{26}}{16 \times \pi \times 3 \times 10^8 \times 6.67 \times 10^{-11} \times 1.99 \times 10^{30} \times 3.5 \times 10^3}$$

$$R = 1.7 \times 10^{-7} m$$

So, we have found out the $R$ for which the dust particle would follow a straight line. If it was any bigger than this $R$, it's mass would be higher and hence the gravitational attraction force will be higher. Any smaller, and the radiation pressure will dominate.

The radiation pressure exerted by the sun is also a radically new method to travel in space. Research to use this as a more viable mechanism over conventional solid/liquid fuel is ongoing.