My Frame, Your Frame

You're probably sitting and reading this piece on the planet we call Earth. But Earth is just an insignificant rock in the vast Solar System we live in, and we have barely sent a couple of tiny metal boxes to the edge of it. This stellar system is again just a tiny system in the humongous Milky Way galaxy. To go a few more orders of magnitude higher while this in itself is quite incomprehensible to our logarithmic minds, we end up as a speck in the Laniakea Supercluster, the home to around a hundred thousand galaxies. How do we pinpoint ourselves in this mess?

Let's say you have an alien friend, who wants the directions to our place. Let's simplify the problem to identifying ourselves in the Milky Way. If our alien shares the same naming conventions as us, we seem good. But it's an awful assumption that they have the same names for every rock, gas ball, and gravity well out there. We stick to something more uniform for us all, something like math. We try to describe our position mathematically and to do so, we will need a coordinate system.

Rectangular Coordinate System

To explore the idea of a coordinate system, let's return to more friendly firm ground on Earth. This is a map of Manhattan, New York, USA.

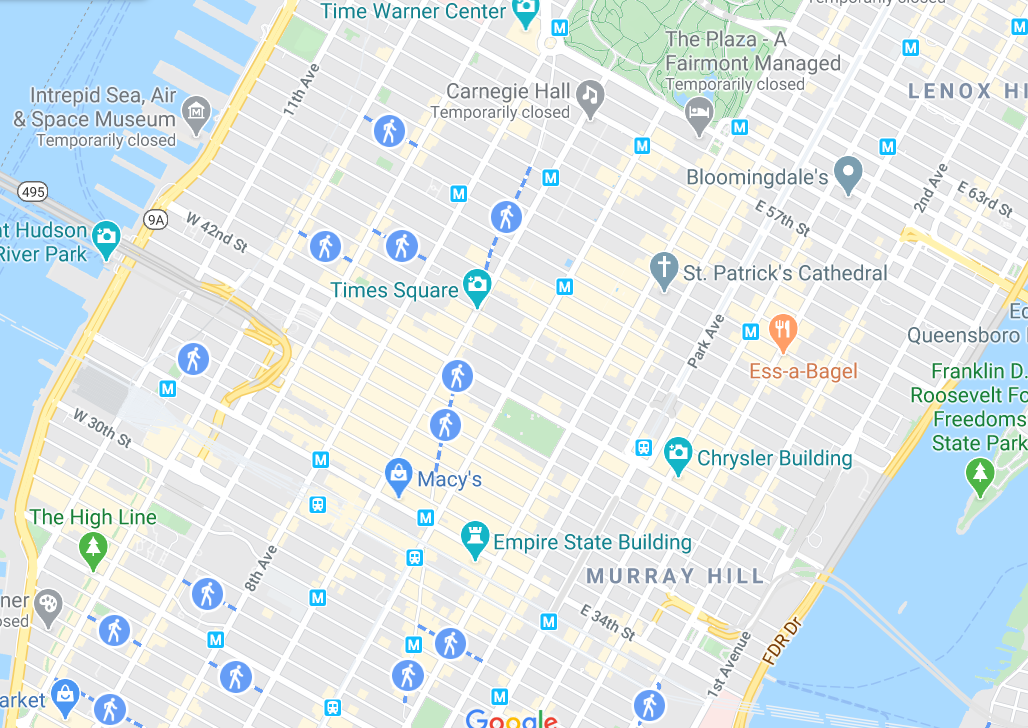
There are nice rectangular streets in the place, so it would be quite easy to locate a person from a bird's eye view. To mark off specific points, we'd first need to use a reference point. Let's consider Times Square, being such a nice central point as our reference. We could have chosen something else too, say for example the Empire State Building, but let's go with Times Square. The road north towards Carnegie hall will serve as one of the axes for our purpose. The other axis will be the road perpendicular to this one, but again passing through Times Square. This leads us to something familiar, the Cartesian coordinate system or the rectangular coordinate system. Only it's rotated a bit. That feels slightly off. Let's consider every road intersection as a point on the coordinate grid in our system that we just defined. This should put St Patrick's Cathedral at $(2.5, 5.5)$. Now, let's rotate the coordinate system so our y-axis faces north in a setting we are more used to (from Times Square along a line slightly to the left of Time Warner Center), but let's keep Times Square as our center, in the origin. Does this change the position of St Patrick's Cathedral? No, only the coordinates change, and with a piece of paper, we can calculate that. The x coordinate slightly increases while the y coordinate reduces to a rather small value. What if we redefine our origin now, and we shift it to the Empire State Building? Again, the position of St Patrick's Cathedral couldn't care less. The only thing we'd have to change is the coordinate value itself. And we can convert between the various systems we define quite easily.

Polar Coordinate System

What if we radically change our view of a coordinate system? Let's take a look at Connaught Place, New Delhi, India.

We can try to attack this problem with a similar approach to the last. We could be anarchists and choose Madame Tussauds as our origin, but let's just pick the center of the Central Park and not be masochistic. Let's say we fancy a nice burger, and want to pinpoint the location of Burger Singh. Assuming the direction of true north as the y-axis and the perpendicular direction as the x-axis, we can try something, but that would have a lot of ugly specific numbers. Can we make our problem simpler? The circles suggest a radial approach to our problem, and that is what we will try. Considering the east as a reference axis, if we rotate a ray around $135^o$ counterclockwise from the axis, we should land on a line with the eatery. We now determine it's on the second circular road from the center, and we have just defined a new coordinate system that works. This is called the polar coordinate system, where instead of representing coordinates as $(x, y)$, we use $(r, \theta)$ to represent our coordinates. The former is a radial coordinate and the latter is an angular coordinate. And as we saw in the Manhattan example, we can switch between the rectangular system and the polar system just as we switched between the systems there.

Returning to our original problem, let's now take a spaceship eye's view of our galaxy. The circular patterns again suggest the polar coordinate system to us. For our origin, we could again choose the center of the galaxy. The reference axis could be the ray from the center to the top of the image. With this, we can say our Solar System should lie in the whereabouts of the point $(\text{Orion-Cygnus Arm}, -45^o)$ give or take a few hundred light-years. But where will we be in a hundred thousand years? The solar system, much like the Earth around the Sun, takes a trip around the center of the galaxy in around 225-250 million years. This poses a small problem for us, we'd have to keep changing our measurement. To keep our coordinate constant, we can instead keep the reference frame moving. Let's change the reference axis to something that's revolving around the center as well, to the ray from the center passing through the tip of the Perseus arm. And this moving reference frame can be used interchangeably with our previous frame making a major assumption - the rotation around the galactic center is uniform.

Inertial Reference Frame

This leads us to our next key idea. Our reference frame can be absolutely anything, provided our coordinates are defined properly. When there is a nice constant velocity, we can simply jump between coordinate systems very easily. This is called a Galilean transformation. This sort of reference frame where everything has a difference of only constant relative motion is called an inertial reference frame. The laws of physics are the exact same in every inertial reference frame. To experience a non-inertial reference frame, just get into an elevator. The jerk the elevator gives you while accelerating, for those fleeting moments, puts you in a non-inertial reference frame. You would experience unfriendly unseen forces, by virtue of the acceleration of your frame. If you step out of the elevator and look at it from the ground, in an inertial reference frame, you would be able to point the different forces out but locked in the elevator, there's no way to really know. Without such complications, the Galilean transformation still suffers a major flaw, which was exposed by the Theory of Special Relativity, and corrected by the Lorentz transformation.

Why is the Galilean transformation incorrect?

Let's consider two reference frames, a stationary one, A, and one moving at a constant velocity in one direction, B. Let's assume a coordinate system for A as $(x, y, z, t)$. This four-vector is used to refer to spacetime or is also known as the Minkowski space. Assuming frame B moves with a velocity of $v$, an observer on frame A would see the observer on frame B move as $x=vt$. Assuming $(x', y', z', t')$ as the corresponding coordinate system for frame B, the conversion from A to B would be straightforward as described by these equations.

$x' = x-vt$

$y' = y$

$z' = z$

$t' = t$

Now let's say there is a light ray from the origin towards B's frame. In the frame of A, it would appear to be moving as $x = ct$. How would it look in the frame of B? Let's use $t'$ to account for time in B's frame. This would mean the ray would appear to move as $x' = ct'-vt'$. So the speed of light would appear to be $c-v$. But with the advent of modern technology and precise measurement techniques, it turns out the speed of light in the frame of B is not $c-v$, but rather just $c$. And we're just getting started.

The Flaw

The Galilean transformation equations were much like Archimedean laws of motion, they were correct with what was observed at the time. With the speed of light being constant in all frames being set in stone both by experiment, and Einstein's theory, we have to now implement a workaround. To do so, we must first capture the flaw. The elusive flaw is the fourth equation in the Galilean transformation. Special relativity changes the very notion of simultaneity and makes it frame-dependent. This idea has also been experimentally verified with atomic clocks and planes, atomic clocks and mountains, to test if the motion of the reference frame actually has an influence on the ticking of time.

Lorentz Transformation

If the Galilean transformation is wrong, how do we jump from frame to frame? We start with an assumption that space-time is the same everywhere, an infinite, unchanging coordinate space. This says that no event is special, and we can choose our origin arbitrarily. We already played around with this idea in Manhattan, let's apply it to the Universe. The Galilean equation does get a few things right, for instance, that $x=vt$ when $x'=0$. We have to modify this to account for speeds, but not lose the linear property of this equation. We'll also make another helpful assumption, let's consider the speed of light, $c$, a constant value as a dimensionless quantity, 1. So now, let's multiply the right side with a function of the velocity.

$x' = (x-vt)f(v)$

But what is $f(v)$? We have another ace up our sleeve. Our function should not be able to discriminate between left and right. This means that we must lock the sign of the velocity in the function, and a simple way to do this is to square the velocity. So now, we have this equation.

$x' = (x-vt)f(v^2)$

In the same way, we can modify our equation to account for the time axis.

$t' = (t-vx)g(v^2)$

Now if we consider the path of a light ray in both the frames, and apply our principle, that the speed of light is constant in all the frames, then we find that $x=t$ and $x'=t'$. From this, we get another beautiful piece of symmetry:

$f(v^2)=g(v^2)$

We have one last piece of symmetry which solves our puzzle. And this is that we can't really say which frame is moving, is the frame B moving with velocity $v$ or is the frame A moving with velocity $-v$? So this means that instead of having $(x, y, z, t)$ for frame A, we could have had $(x', y', z', t')$.

Now we can just cross substitute values to give us these twin equations.

$x=(x'+vt')f(v^2)$

$t = (t'+vx')f(v^2)$

With some algebra, we can solve for $f(v^2)$.

$f(v^2) = \frac{1}{\sqrt{1-v^2}}$

Finally, we get in the prized Lorentz transformation, the heir to the throne.

$x'=\frac{x-vt}{\sqrt{1-v^2}}$

$t' = \frac{t-vx}{\sqrt{1-v^2}}$

To go back to our old unit system with which we've gotten so used to, all we need to do is ensure our equations are dimensionally consistent, and having taken $c$ as 1, we need to make these changes:

$x' = \frac{x-vt}{\sqrt{1-\frac{v^2}{c^2}}}$

$t' = \frac{t-\frac{v}{c^2}x}{\sqrt{1-\frac{v^2}{c^2}}}$

For small friendly values of $v$, these equations can be approximated back to the Galilean equations. But for large values, when $v$ is comparable with $c$, these changes become quite drastic. Now we can try to be sneaky and plug in super large values of $c$. If $v$ happens to be greater than c, we end up with imaginary values which is crazy. So we put forward another rule. No object can move faster than light.

The cool idea here is that we don't have to stretch out too many axes and get lost in a muddle of algebra. If we want to jump from one axis to another, first we start by rotating the axes, and align them. Now a simple Lorentz transformation along the new x axis to get us up to speed, and we can just unrotate the rotation to restore the original orientation.

We've just taken our first step into a larger, paradoxical, fun world.