Energy of a Body under a Gravitational Trajectory

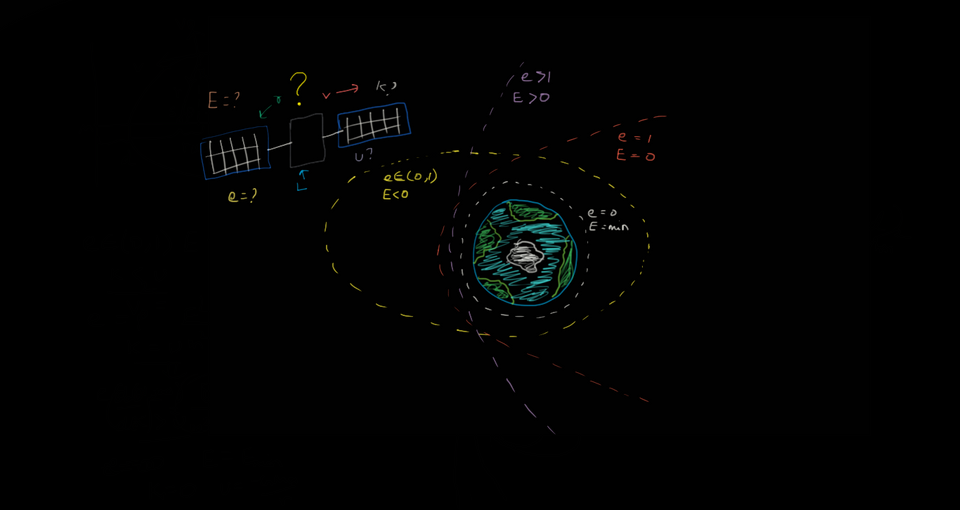
This is just one long derivation. Seriously. But wait! Don't go! Watch these first:

And this one:

So in the second video, I showed you how the trajectories are conics. But I made ANOTHER assumption, and you just took my word for it. So, here's the energy and trajectory derivation. This was called the Kepler's problem and this relates to Kepler's Third Law.

The first step is reducing our work. Gravity acts between two bodies. We, humans, being naturally lazy have this brilliant step to reduce this to a single body problem. So we did this:

$$\frac{1}{\mu} = \frac{1}{m_1} + \frac{1}{m_2}$$

The motion of two bodies which are interacting via a gravitational force is equivalent to the motion of a single body acted on by an external central gravitational force. The mass of the single body is called the reduced mass and is represented by µ. If we solve for the motion of µ in this one-body situation, we can then return to the two-body interaction and solve for the actual motion of the two original bodies.

The motion of the reduced mass has two constants, its total energy E and its angular momentum L about the origin O . Energy is a constant because in the two-body problem, the gravitational force is an internal conservative force. Angular momentum about the origin is constant because the only force is directed towards the origin. So, the torque about the origin due to that force must be zero. As the angular momentum is constant, the orbit of the reduced mass lies on a plane with the angular momentum vector pointing out of this plane. Now we have to choose polar coordinates for our body like this:

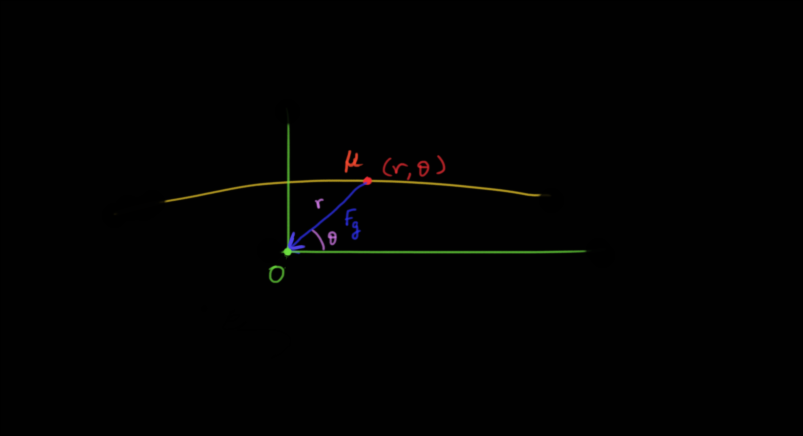
The total energy $E$ of the body will be given by

$$E = \frac{1}{2} \mu v^2 - \frac{G M m}{r}$$

We know choose polar coordinates such that

$$\vec{v} = v_r \hat{r} + v_\theta \hat{\theta}$$

$$v_r = \frac{dr}{dt}$$ and $$v_\theta = r \frac{d\theta}{dt}$$

So now, our $E$ becomes

$$E = \frac{1}{2} \mu \left( \left( \frac{dr}{dt} \right) ^2 + \left( r \frac{d\theta}{dt} \right) ^2 \right) - \frac{GMm}{r}$$

Angular Momentum with respect to the origin is given by

$$\vec{L_O} = \mu r^2 \frac{d\theta}{dt} \hat{k}$$

We can now eliminate $θ$ from the energy equation

$$E = \frac{1}{2} \mu \left(\frac{dr}{dt}\right)^2 + \frac{1}{2} \frac{L^2}{\mu r^2} - \frac{GMm}{r}$$

If we rearrange this for $\frac{dr}{dt}$, and divide this from our previous expression for $\frac{dθ}{dt}$

$$\frac{d\theta}{dr} = \frac{L}{\sqrt{2 \mu}} \frac{1/r^2}{\sqrt{E - \frac{L^2}{2 \mu r^2} + \frac{GMm}{r}}}$$

As r and θ are separable, they can be integrated to find r as a function of θ. The result is the orbit equation. This is given by

$$r = \frac{r_0}{1 - e cos\theta}$$

The semilatus rectum is given by

$$r_0 = \frac{L^2}{\mu GMm}$$

Thus finally, a culmination of this hard work gives us the expression for eccentricity,

$$e = \sqrt{1+ \frac{2 E L^2}{\mu (GMm)^2}}$$

From this, we can specifically find the equations of the orbit at different eccentricities, which correspond to different energies. It is shown that these are the circle, the ellipse, the parabola and the hyperbola in the second video.

And as mentioned in the first video, the spacecraft "Fury" attained extreme velocities, and its trajectory looked like a straight line. Its not hard to see that this is the case if v is very high, so is E and as a result so is e. Thus, as they tend to higher values, e tends to infinity, giving the straight line.