The Direction of Time

Time, as we all know is a scalar. If a quantity is a scalar, then it has only magnitude and no direction. But time is directional (and so is electric current). What makes it move forward? Why don't some things happen backwards, like the playback of a video?

Let's start off with irreversible processes. Certain processes can never happen backward, such as the curdling of milk or the diffusion of a gas in a room. Curd can't be converted back to the milk that it was made with and the gas molecules can't be collected back to get the original gas.

The one-way, irreversible character of these processes is so pervasive that we take it for granted. If these processes were to happen backward, we would be shocked and amazed. However, the Law of Conservation of Energy, one of the fundamental laws of physics, won't be violated if one of these irreversible changes went backward. From this, it is obvious that the change in energy of a system doesn't set the direction of a process. Instead, it depends on a different quantity, called entropy. Entropy is the measure of randomness. Unlike energy, entropy does not have a conservation law. The Second Law of Thermodynamics states that the entropy of a system can never decrease, it either remains constant or increases. If an irreversible process went backward, then, in violation of the law stated above, the entropy would decrease. Therefore, it never happens.

One of the ways of measuring the change in entropy of a system is in terms of its temperature and the energy it gains or loses as heat. Let's take the example of diffusion of a gas. Diffusion is an example of free expansion. Consider two containers out of which one is a vacuum and the other is filled with a gas. Let the containers be connected by the means of a closed tube. If we open the connection between the containers, gas spontaneously flows from the filled container to the vacuum. This is an irreversible process and the molecules of gas will never return back to the container they came from.

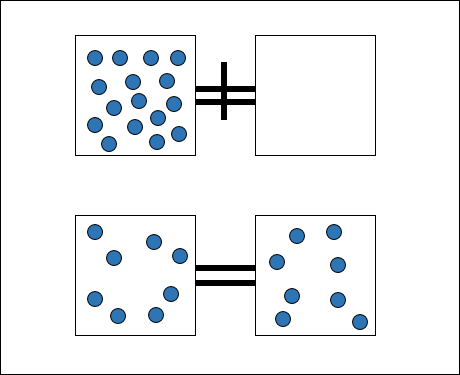
Pressure and Volume of a gas are its state properties, properties that depend only on the state of the gas. Other state properties are temperature and energy. The change in entropy of a system after it undergoes the above process is given by

$$ \Delta S = S_f - S_i = \frac{Q}{T}$$

where Q is the energy transferred as heat from or to the system and T is its temperature.

It can be proved that entropy is also a state function for the special case where an ideal gas is taken through a reversible process. The process is done slowly, in small steps. Let the energy transferred in each step be dQ, the work done by the gas be dW and the change in internal energy be dE.

$$ dE = dQ - dW$$

As these steps are reversible, and

$$ dE = nC_V \ dT$$

$$ dW = p \ dV $$

$$ dQ = p \ dV + nC_V \ dT $$

From the ideal gas law,

$$ p = \frac{nRT}{V} $$

and by dividing our equation by T on both sides, we get

$$ \frac{dQ}{T} = \frac{nR \ dV}{V} + nC_V \frac{dT}{T} $$

Integrating this from an initial state i to a final state f, we get

$$ \Delta S = nR \ \text{ln} (\frac{V_f}{V_i}) + nC_V \ \text{ln} (\frac{T_f}{T_i}) $$

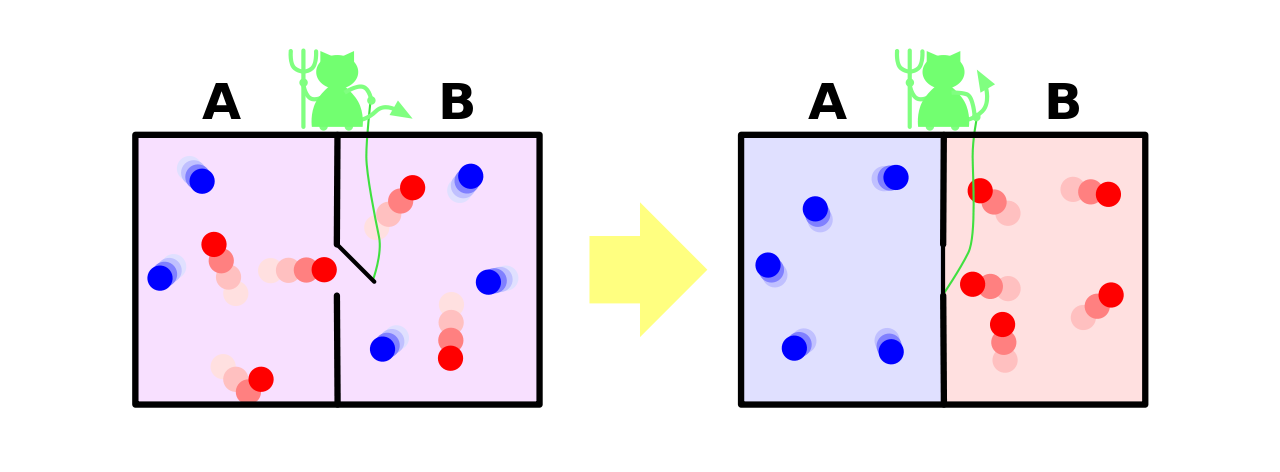
Let me finish with a thought experiment. Consider our case of the containers again. This time, we have someone in control of the tube between the containers who can open it and close it for very small instants of time. This person opens it and closes it in such a way that the faster molecules are collected in one side and the slower molecules are collected in another side. The side having the faster molecules will undoubtedly have a higher temperature than the other side due to higher kinetic energy. This person controlling the tube was called Maxwell's Demon. It was a product of a thought experiment by James Clerk Maxwell in 1867 and was given the term demon by William Thomson (Lord Kelvin). But does this violate the Second Law of  Thermodynamics?

If you want to explore entropy further, do so by checking out the video below.